Witam. Dzisiaj przeprowadzę krótką analizę nagród na turniejach typu premier draft na Arenie. Premier draft polega na tym, że po standardowym drafcie gramy aż do 7 wygranych lub do 3 przegranych, zależy co nastąpi pierwsze. Nagrody dostajemy w zależności od liczby zwycięstw.
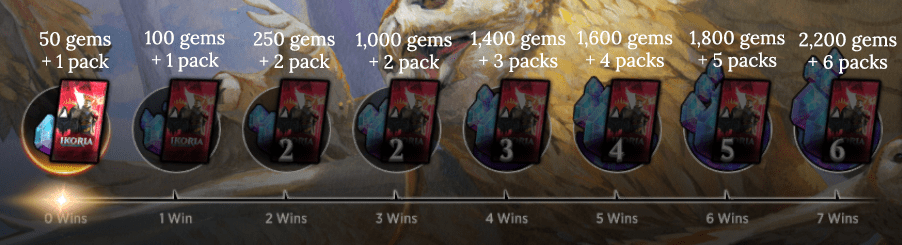
Dzisiaj obliczymy parę statystyk, takich jak oczekiwana nagroda za wzięcie udziału w premier drafcie lub też potrzebny procent zwycięstw, aby oczekiwana nagroda pozwalała na ponowne wkupienie się do turnieju.
Trochę matematyki
Każdy gracz ma pewne prawdopodobieństwo wygrania gry, oznaczymy je przez p. Grając dużo gier, możemy oszacować je przez liczbę wygranych gier podzieloną przez liczbę zagranych przez nas meczy. Amator rozgrywki MTG będzie miał p mniejsze niż 1/2, gdyż wygrywa mniej niż połowę spotkań. Profesjonaliści osiągają p > 0.6, czyli wygrywają ponad 3 z 5 zagranych gier. W zależności od tej właśnie liczby będziemy obliczać oczekiwaną nagrodę. Oznaczmy przez K liczbę maksymalnie wygranych spotkań. Co prawda K jest równe po prostu 7, ale wydaje mi się, że to oznaczenie pozwala na lepszą czytelność. Aby obliczyć wartość oczekiwaną z gry w premier drafcie, potrzebujemy prawdopodobieństwa wygrania dokładnie k meczy, gdzie 0 <= k <= K. Oznaczmy więc:
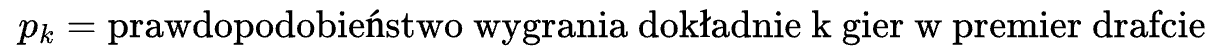
Jeżeli nie zdobyliśmy trofeum w tym drafcie, tzn. k < K, to musieliśmy przegrać trzy mecze, w tym ostatni. Zagraliśmy więc dokładnie k + 3 mecze, z czego ostatni jest porażką, a dodatkowo przegraliśmy pewne dwa spośród pierwszych k + 2 meczy. Mamy więc:
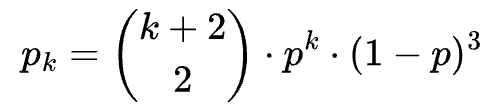
Jeżeli zdobyliśmy trofeum w tym drafcie, tzn. k = K, to mamy trzy przypadki: wygraliśmy wszystko, przegraliśmy jeden mecz (nie może być to mecz ostatni) lub przegraliśmy dwa mecze (nie może być to mecz ostatni). Prawdopodobieństwo to wyraża się więc wzorem:
Liczba zwycięstw w zależności od p
W tym momencie możemy już zobaczyć rozkład liczby zwycięstw w zależności od p. Pokażę go dla p = 0.4 (amator), p = 0.5 (przeciętniak) i p = 0.6 (dobry gracz).
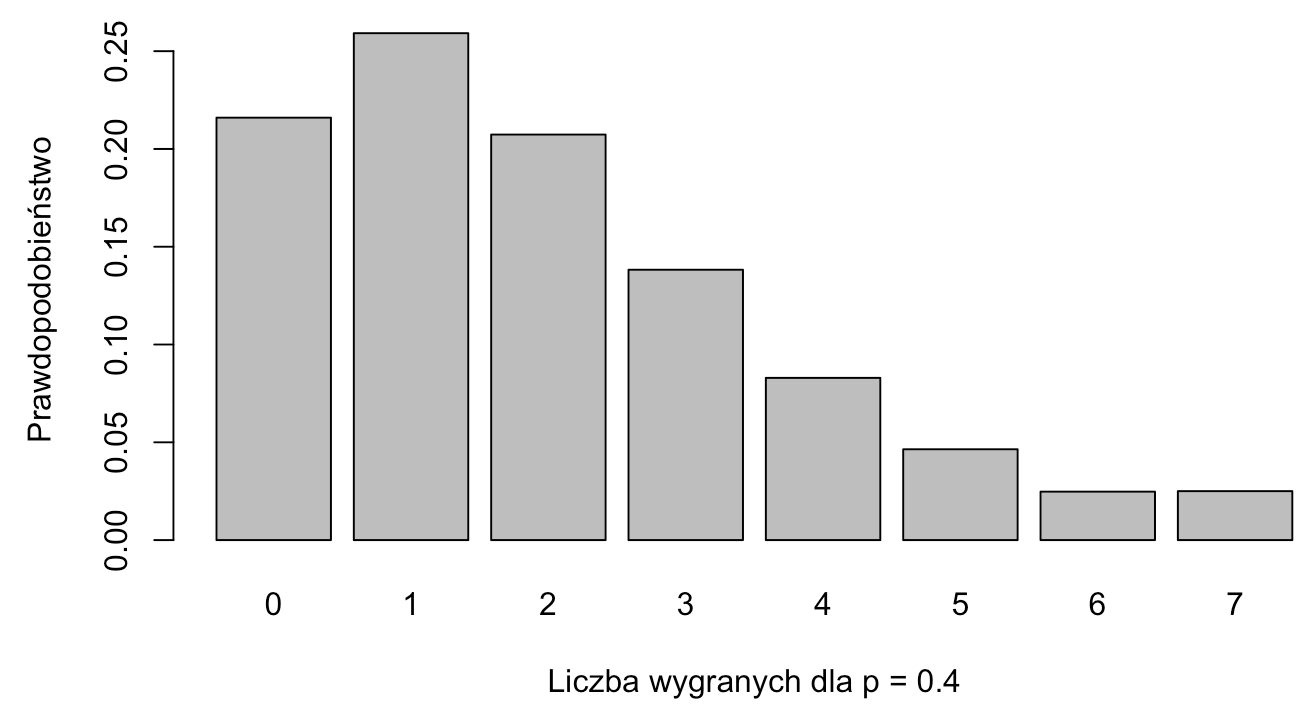
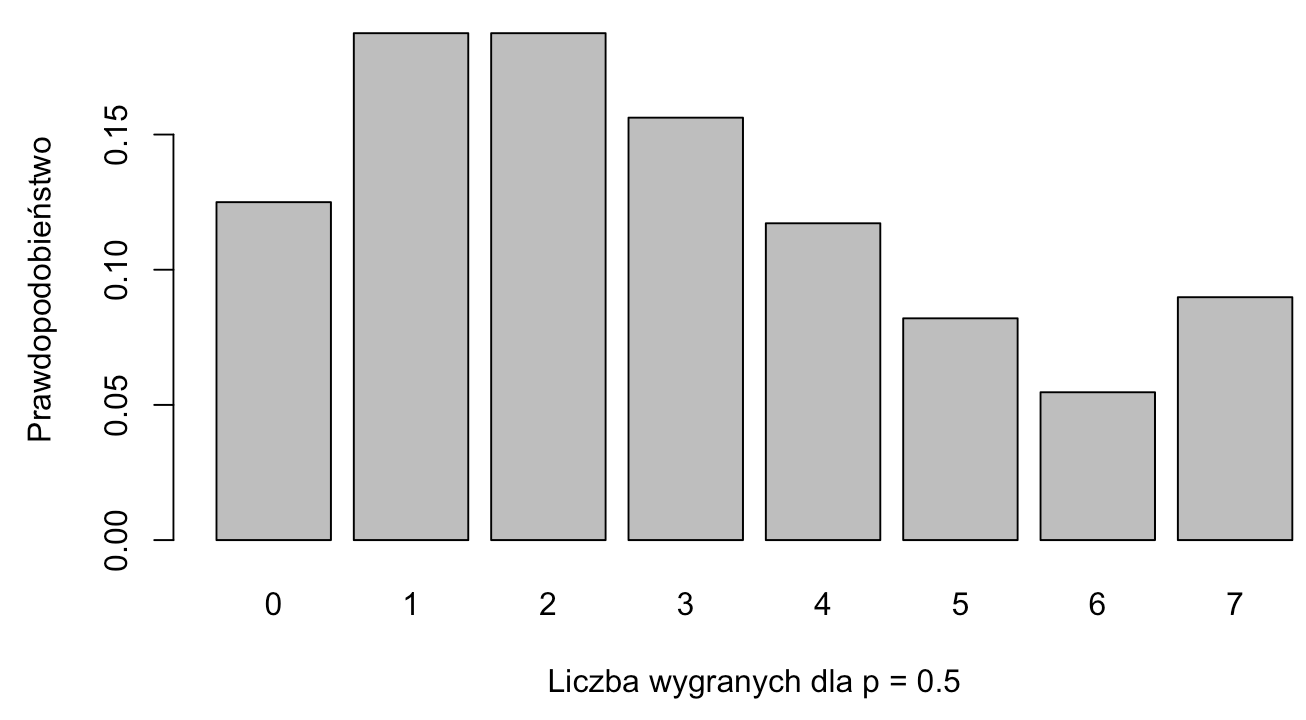
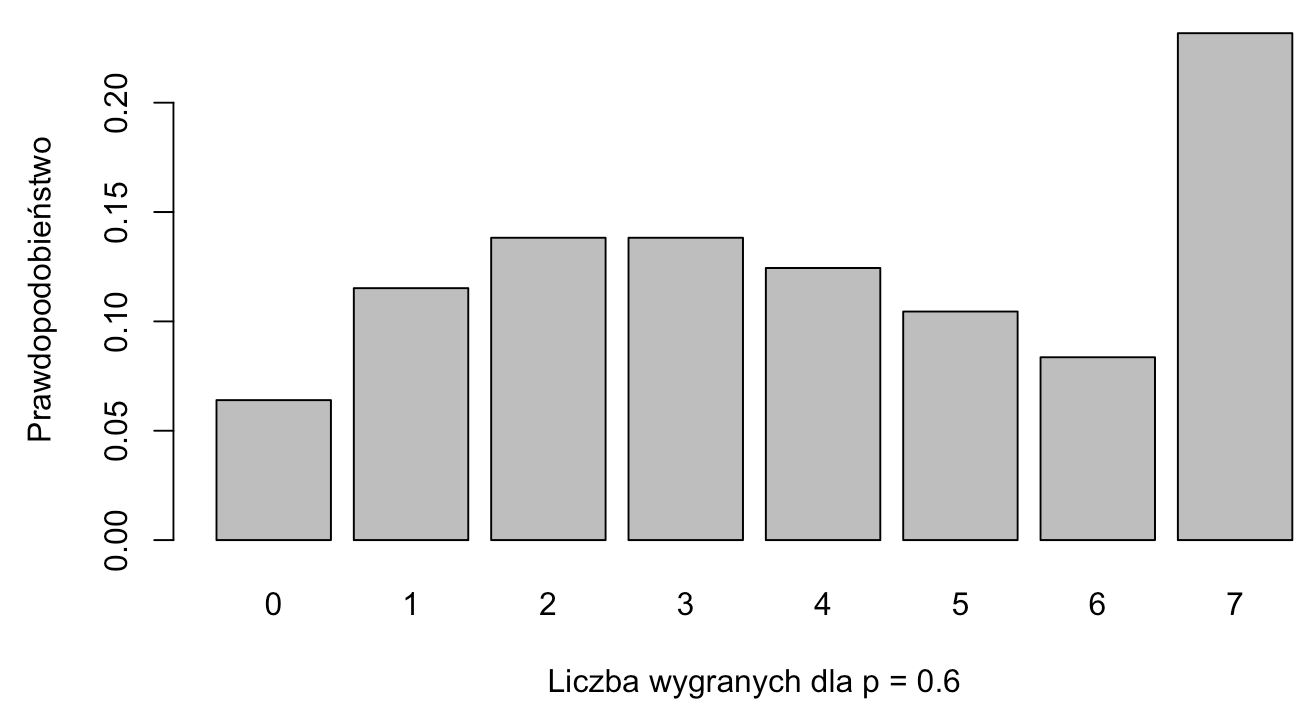
Jak widzimy, życie nie wygląda kolorowo dla amatora, ale rozkłady dla przeciętniaka i dobrego gracza wyglądają obiecująco. Prawodpodobieństwo wygrania trofeum jest duże, nawet w przypadku przeciętniaka większe niż prawdopodobieństwo wygrania 5 czy też 6 meczy. Niewątpliwie częste zdobywanie trofeum przekłada się na dużą dawkę dopaminy.
Oczekiwana liczba zdobytych gemów
Możemy się więc zastanowić, jak wygląda oczekiwana liczba zdobytych gemów w zależności od p. Wartość oczekiwana to suma iloczynów prawdopodobieństwo razy liczba wygranych gemów. Od uzyskanej wartości odejmuję wpisowe 1500 gemów.
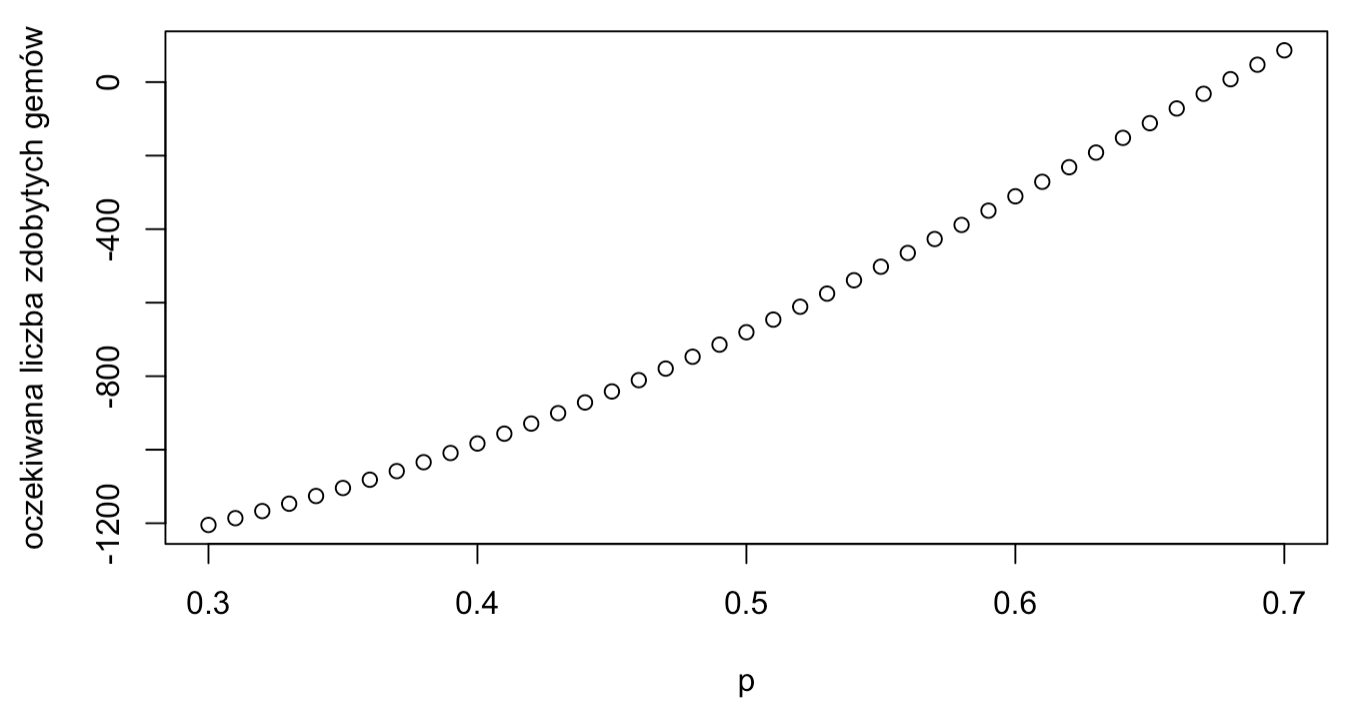
Jak widzimy, zależność oczekiwanej liczby zdobytych gemów od p jest praktycznie liniowa. Niestety jest ona grubo poniżej 0, nawet w przypadku graczy o winrate większym niż 0.6. Z tego co widzimy, gracz z p = 1/2 traci średnio 681 gemów co turniej, a gracz z p = 0.6 około 310.
Jaki winrate jest potrzebny, aby statystycznie móc za wygraną wkupić się w kolejny turniej?
Z moich wyliczeń wynika, że aby móc raz zakupić gemy i potem tylko wkupywać się na kolejne turnieje, trzeba mieć winrate na poziomie 67,8%. Oznacza to, że nawet gracze wygrywający 2 na 3 gry będą z czasem tracić gemy.
Na pieniądze
3400 gemów kosztuje 100PLN. Oznacza to, że gracz o winrate 0.4 traci statystycznie 28.91PLN co turniej, gracz o winrate 0.5 – 20.01PLN, a gracz o winrate 0.6 – 9.13PLN. Oczywiście nie wliczam w to wygranych takich jak paczki, realna wartość oczekiwana może być inna dla graczy, którzy grają constructed na Arenie.
Wniosek
Gracz średni, o winrate 0.5, średnio traci 45%, co jest dużo więcej niż dowolna inna gra hazardowa. Przed odpaleniem areny polecam więc dwa razy zastanowić się, czy nie lepiej pograć na Plinko (najlepiej u Buddy).
PS
Jakby kogoś interesowały inne statystyki, takie jak oczekiwana liczba wygranych paczek, bądź też jej odchylenie standardowe, zapraszam na priv.
a jest jakieś tldr dla humanistów?
nie graj na arenie bo stracisz sousiwo👀